Предел функции — MT1205: Математический анализ для экономистов — Бизнес-информатика. Определение бесконечно большой функции Функция называется бесконечно малой

БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ ОСНОВНЫЕ СВОЙСТВА

Функция y=f(x) называется бесконечно малой при x→a или при x →∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Примеры.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .

Обратно, если , то f (x)=b+α(x) , где a(x) – бесконечно малая при x→a.

Доказательство .

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство . Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x) , где и . Нам нужно доказать, что при произвольном как угодно малом ε> 0 найдется δ> 0, такое, что для x , удовлетворяющих неравенству |x – a|<δ , выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε> 0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ 1 > 0, что при |x – a|< δ 1 имеем |α(x)|< ε/ 2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ 2 > 0, что при |x – a|< δ 2 имеем | β(x)|< ε/ 2.

Возьмем δ=min{ δ 1 , δ 2 } .Тогда в окрестности точки a радиуса δ будет выполняться каждое из неравенств |α(x)|< ε/ 2 и | β(x)|< ε/ 2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x) | ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|< ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞ ) есть бесконечно малая функция.

Доказательство . Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a , то для произвольного ε> 0 найдется окрестность точки a , в которой будет выполняться неравенство |α(x)|< ε/M . Тогда в меньшей из этих окрестностей имеем | αf|< ε/M = ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

Следствие 1. Если и , то .

Следствие 2. Если и c= const, то .

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x) , предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство . Пусть . Тогда 1/f(x) есть ограниченная функция. Поэтому дробь есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ

Теорема 1. Если функция f(x) является бесконечно большой при x→a , то функция 1/f(x) является бесконечно малой при x→a .

Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x , для которых |x – a|<δ , выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a , то найдется δ>0 такое, что как только |x – a|<δ , так |f(x)|> 1/ ε. Но тогда для тех же x .

Примеры.

Можно доказать и обратную теорему.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y= 1/f(x) является бесконечно большой функцией.

Доказательство теоремы проведите самостоятельно.

Примеры.

Таким образом, простейшие свойства бесконечно малых и бесконечно больших функций можно записать с помощью следующих условных соотношений: A ≠ 0

ТЕОРЕМЫ О ПРЕДЕЛАХ

Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа функций равен алгебраической сумме пределов этих функций, т.е.

Доказательство . Проведем доказательство для двух слагаемых, так как для любого числа слагаемых оно проводится так же. Пусть .Тогда f(x)=b+α(x) и g(x)=c+β(x) , где α и β – бесконечно малые функции. Следовательно,

f(x) + g(x)=(b + c) + (α(x) + β(x)) .

Так как b + c есть постоянная величина, а α(x) + β(x) – функция бесконечно малая, то

Пример. .

Теорема 2. Предел произведения двух, трех и вообще конечного числа функций равен произведению пределов этих функций:

Доказательство . Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) и

fg = (b + α)(c + β) = bc + (bβ + cα + αβ).

Произведение bc есть величина постоянная. Функция bβ + c α + αβ на основании свойств бесконечно малых функций есть величина бесконечно малая. Поэтому .

Следствие 1. Постоянный множитель можно выносить за знак предела:

.

Следствие 2. Предел степени равен степени предела:

.

Пример. .

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля, т.е.

.

Доказательство . Пусть . Следовательно, f(x)=b+α(x) и g(x)=c+β(x) , где α, β – бесконечно малые. Рассмотрим частное

Дробь является бесконечно малой функцией, так как числитель есть бесконечно малая функция, а знаменатель имеет предел c 2 ≠0.

Примеры.

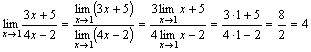
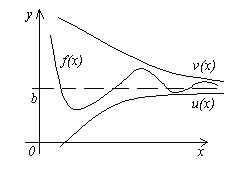
Теорема 4. Пусть даны три функции f(x), u(x) и v(x) , удовлетворяющие неравенствам u(x)≤f(x)≤ v(x) . Если функции u(x) и v(x) имеют один и тот же предел при x→a (или x→∞ ), то и функция f(x) стремится к тому же пределу, т.е. если

, то .

Смысл этой теоремы понятен из рисунка.

Доказательство теоремы 4 можно найти, например, в учебнике: Пискунов Н. С. Дифференциальное и интегральное исчисления, т. 1 – М.: Наука, 1985.

Теорема 5. Если при x→a (или x→∞ ) функция y=f(x) принимает неотрицательные значения y≥0 и при этом стремится к пределу b , то этот предел не может быть отрицательным: b≥0 .

Доказательство . Доказательство проведем методом от противного. Предположим, что b<0 , тогда |y – b|≥|b| и, следовательно, модуль разности не стремится к нулю при x→a . Но тогда y не стремится к пределу b при x→a , что противоречит условию теоремы.

Теорема 6. Если две функции f(x) и g(x) при всех значениях аргумента x удовлетворяют неравенству f(x)≥ g(x) и имеют пределы , то имеет место неравенство b≥c .

Доказательство. По условию теоремы f(x)-g(x) ≥0 , следовательно, по теореме 5 , или .

ОДНОСТОРОННИЕ ПРЕДЕЛЫ

До сих пор мы рассматривали определение предела функции, когда x→a произвольным образом, т.е. предел функции не зависел от того, как располагалось x по отношению к a , слева или справа от a . Однако, довольно часто можно встретить функции, которые не имеют предела при этом условии, но они имеют предел, если x→a , оставаясь с одной стороны от а , слева или справа (см. рис.). Поэтому вводят понятия односторонних пределов.

Если f(x) стремится к пределу b при x стремящемся к некоторому числу a так, что x принимает только значения, меньшие a , то пишут и называют bпределом функции f(x) в точке a слева.

Определение числовой функции. Способы задания функций.

Пусть D – множество на числовой прямой R. Если каждому х принадлежащему D поставлено в соответствие единственное число y=f(x), то говорят, что задана функция f.

Способы задания функций:

1) табличный – для функций, заданных на конечном множестве.

2) аналитический

3) графический

2 и 3 – для функций, определенных на бесконечном множестве.

Понятие обратной функции.

Если функция y=f(x) такова, что разным значениям х аргумента соответствуют разные значения у функции, то переменную х можно выразить как функцию переменной у: x=g(y). Функцию g называют обратной к f и обозначают f^(-1).

Понятие сложной функции.

Сложная функция- функция, аргументом которой является другая любая функция.

Пусть даны функции f(x) и g(x). Составим из них две сложные функции. Считая функцию f внешней (главной), а функцию g – внутренней, получаем сложную функцию u(x)=f(g(x)).

Определение предела последовательности.

Число а называется пределом последовательности {xn}, если для любого положительного существует номер n0, начиная с которого все члены посл-ти отличаются от а по модулю меньше, чем на ε (т.е. попадают в ε-окрестность точки а):

Правила вычисления пределов сходящихся последовательностей.

1.Всякая сходящаяся последовательность имеет только один предел. 2. Если все элементы последовательности {x n } равны С (постоянной), то предел последовательности {x n }, тоже равен С. 3. ; 4. ; 5. .

Определение ограниченной последовательности.

Посл-ть {x n } называется ограниченной, если множество чисел X={x n } ограниченно: .

Определение бесконечно малой последовательности.

Посл-ть {x n } наз-ют бесконечно малой, если для любого (сколь угодно малого) >0 найдется такой номер n 0 , что для всякого n>n 0 выполняется нерав-во |x n |< .

Определение бесконечно большой последовательности.

Посл-ть наз-ют бесконечно большой, если для любого (сколь угодно большого) числа А>0 найдется такой номер n 0 , что для всякого номера n>n 0 выполняется нерав-во |x n |>A.

Определение монотонных последовательностей.

Монотонные посл-ти: 1) возрастающая, еслиx n x n +1 для всех n, 4) невозрастающей, еслиx n x n +1 для всех n.

Определение предела функции в точке.

Пределом ф-ии y=f(x) в точке x 0 (или при x x 0) наз-ют число а, если для любой посл-ти{x n } значений аргумента, сходящейся к х 0 (при этом все x n x 0), посл-ть {f(x n)} значений ф-ии сходится к пределу а.

Определение бесконечно малой функции.

Ф-ия f(x) наз-ся бесконечно малой при х→А, если .

Определение бесконечно большой функции.

Ф-ия f(x) наз-ся бесконечно большой при х→А, если .

Приводится определение бесконечно большой последовательности. Рассмотрены понятия окрестностей бесконечно удаленных точек. Дано универсальное определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам. Рассмотрены примеры применения определения бесконечно большой последовательности.

Содержание

См. также: Определение предела последовательности

Определение

Последовательность { β n } называется бесконечно большой последовательностью , если для любого, сколь угодно большого числа M , существует такое натуральное число N M , зависящее от M , что для всех натуральных n > N M выполняется неравенство
|β n | > M .
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности, или сходится к бесконечности .

Если , начиная с некоторого номера N 0 , то
( сходится к плюс бесконечности ).
Если же , то
( сходится к минус бесконечности ).

Запишем эти определения с помощью логических символов существования и всеобщности:
(1) .
(2) .
(3) .

Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.

Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.

Во многих учебниках по математическому анализу, в определении бесконечно большой последовательности указывается, что число M является положительным: M > 0 . Однако это требование является лишним. Если его отменить, то никаких противоречий не возникает. Просто малые или отрицательные значения для нас не представляют никакого интереса. Нас интересует поведение последовательности при сколь угодно больших положительных значениях M . Поэтому, если возникнет необходимость, то M можно ограничить снизу любым, наперед заданным числом a , то есть считать, что M > a .

Когда же мы определяли ε - окрестность конечной точки, то требование ε > 0 является важным. При отрицательных значениях, неравенство вообще не может выполняться.

Окрестности бесконечно удаленных точек

Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.

Пусть M - произвольное число.
Окрестностью точки "бесконечность" , , называется множество .
Окрестностью точки "плюс бесконечность" , , называется множество .
Окрестностью точки "минус бесконечность" , , называется множество .

Строго говоря, окрестностью точки "бесконечность" является множество
(4) ,
где M 1 и M 2 - произвольные положительные числа. Мы будем использовать первое определение, , поскольку оно проще. Хотя, все сказанное ниже, также справедливо и при использовании определения (4).

Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.

Универсальное определение предела последовательности .
Точка a (конечная или бесконечно удаленная) является пределом последовательности , если для любой окрестности этой точки существует такое натуральное число N , что все элементы последовательности с номерами принадлежат этой окрестности.

Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.

Свойство окрестности сходящейся последовательности
Для того, чтобы точка a (конечная или бесконечно удаленная) являлась пределом последовательности , необходимо и достаточно, чтобы за пределами любой окрестности этой точки находилось конечное число членов последовательности или пустое множество.
Доказательство .

Также иногда вводят понятия ε - окрестностей бесконечно удаленных точек.
Напомним, что ε - окрестностью конечной точки a называется множество .
Введем следующее обозначение. Пусть обозначает ε - окрестность точки a . Тогда для конечной точки,
.
Для бесконечно удаленных точек:
;
;
.
Используя понятия ε - окрестностей, можно дать еще одно универсальное определение предела последовательности:

Точка a (конечная или бесконечно удаленная) является пределом последовательности , если для любого положительного числа ε > 0 существует такое натуральное число N ε , зависящее от ε , что для всех номеров n > N ε члены x n принадлежат ε - окрестности точки a :
.

С помощью логических символов существования и всеобщности, это определение запишется так:
.

Примеры бесконечно больших последовательностей

Пример 1

.

.
Выпишем определение бесконечно большой последовательности:
(1) .
В нашем случае
.

Вводим числа и , связав их неравенствами:
.
По свойствам неравенств , если и , то
.
Заметим, что при это неравенство выполняется для любых n . Поэтому можно выбрать и так:
при ;
при .

Итак, для любого можно найти натуральное число , удовлетворяющее неравенству . Тогда для всех ,
.
Это означает, что . То есть последовательность является бесконечно большой.

Пример 2

Пользуясь определением бесконечно большой последовательности показать, что
.

(2) .
Общий член заданной последовательности имеет вид:
.

Вводим числа и :
.
.

Тогда для любого можно найти натуральное число, удовлетворяющее неравенству , так что для всех ,
.
Это означает, что .

.

Пример 3

Пользуясь определением бесконечно большой последовательности показать, что
.

Выпишем определение предела последовательности, равному минус бесконечности:
(3) .
Общий член заданной последовательности имеет вид:
.

Вводим числа и :
.
Отсюда видно, что если и , то
.

Поскольку для любого можно найти натуральное число, удовлетворяющее неравенству , то
.

При заданном , в качестве N можно взять любое натуральное число, удовлетворяющее следующему неравенству:
.

Пример 4

Пользуясь определением бесконечно большой последовательности показать, что
.

Выпишем общий член последовательности:
.
Выпишем определение предела последовательности, равному плюс бесконечности:
(2) .

Поскольку n есть натуральное число, n = 1, 2, 3, ... , то
;
;
.

Вводим числа и M , связав их неравенствами:
.
Отсюда видно, что если и , то
.

Итак, для любого числа M можно найти натуральное число, удовлетворяющее неравенству . Тогда для всех ,
.
Это означает, что .

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

См. также:

Бесконечно малые функции

Функцию %%f(x)%% называют бесконечно малой (б.м.) при %%x \to a \in \overline{\mathbb{R}}%%, если при этом стремлении аргумента предел функции равен нулю.

Понятие б.м. функции неразрывно связано с указанием об изменении ее аргумента. Можно говорить о б.м. функции при %%a \to a + 0%% и при %%a \to a - 0%%. Обычно б.м. функции обозначают первыми буквами греческого алфавита %%\alpha, \beta, \gamma, \ldots%%

Примеры

1. Функция %%f(x) = x%% является б.м. при %%x \to 0%%, поскольку ее предел в точке %%a = 0%% равен нулю. Согласно теореме о связи двустороннего предела с односторонними эта функция — б.м. как при %%x \to +0%%, так и при %%x \to -0%%.
2. Функция %%f(x) = 1/{x^2}%% — б.м. при %%x \to \infty%% (а также при %%x \to +\infty%% и при %%x \to -\infty%%).

Отличное от нуля постоянное число, сколь бы оно ни было мало по абсолютному значению, не является б.м. функцией. Для постоянных чисел исключение составляет лишь нуль, поскольку функция %%f(x) \equiv 0%% имеет нулевой предел.

Теорема

Функция %%f(x)%% имеет в точке %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой конечный предел, равный числу %%b%%, тогда и только тогда, когда эта функция равна сумме этого числа %%b%% и б.м. функции %%\alpha(x)%% при %%x \to a%%, или $$ \exists~\lim\limits_{x \to a}{f(x)} = b \in \mathbb{R} \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_{x \to a}{\alpha(x) = 0}\right). $$

Свойства бесконечно малых функций

По правилам предельного перехода при %%c_k = 1~ \forall k = \overline{1, m}, m \in \mathbb{N}%%, следуют утверждения:

1. Сумма конечного числа б.м. функций при %%x \to a%% есть б.м. при %%x \to a%%.
2. Произведение любого числа б.м. функций при %%x \to a%% есть б.м. при %%x \to a%%.

Произведение б.м. функций при %%x \to a%% и функции, ограниченной в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки а, есть б.м. при %%x \to a%% функция.

Ясно, что произведение постоянной функции и б.м. при %%x \to a%% есть б.м. функция при %%x \to a%%.

Эквивалентные бесконечно малые функции

Бесконечно малые функции %%\alpha(x), \beta(x)%% при %%x \to a%% называются эквивалентными и пишутся %%\alpha(x) \sim \beta(x)%%, если

$$ \lim\limits_{x \to a}{\frac{\alpha(x)}{\beta(x)}} = \lim\limits_{x \to a}{\frac{\beta(x)}{\alpha(x)}} = 1. $$

Теормема о замене б.м. функций эквивалентными

Пусть %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% — б.м. функции при %%x \to a%%, причем %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, тогда $$ \lim\limits_{x \to a}{\frac{\alpha(x)}{\beta(x)}} = \lim\limits_{x \to a}{\frac{\alpha_1(x)}{\beta_1(x)}}. $$

Эквивалентные б.м. функции.

Пусть %%\alpha(x)%% — б.м. функция при %%x \to a%%, тогда

1. %%\sin(\alpha(x)) \sim \alpha(x)%%
2. %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac{\alpha^2(x)}{2}%%
3. %%\tan \alpha(x) \sim \alpha(x)%%
4. %%\arcsin\alpha(x) \sim \alpha(x)%%
5. %%\arctan\alpha(x) \sim \alpha(x)%%
6. %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
7. %%\displaystyle\sqrt[n]{1 + \alpha(x)} - 1 \sim \frac{\alpha(x)}{n}%%
8. %%\displaystyle a^{\alpha(x)} - 1 \sim \alpha(x) \ln(a)%%

Пример

$$ \begin{array}{ll} \lim\limits_{x \to 0}{ \frac{\ln\cos x}{\sqrt{1 + x^2} - 1}} & = \lim\limits_{x \to 0}{\frac{\ln(1 + (\cos x - 1))}{\frac{x^2}{4}}} = \\ & = \lim\limits_{x \to 0}{\frac{4(\cos x - 1)}{x^2}} = \\ & = \lim\limits_{x \to 0}{-\frac{4 x^2}{2 x^2}} = -2 \end{array} $$

Бесконечно большие функции

Функцию %%f(x)%% называют бесконечно большой (б.б.) при %%x \to a \in \overline{\mathbb{R}}%%, если при этом стремлении аргумента функция имеет бесконечный предел.

Подобно б.м. функциям понятие б.б. функции неразрывно связано с указанием об изменении ее аргумента. Можно говорить о б.б. функции при %%x \to a + 0%% и %%x \to a - 0%%. Термин “бесконечно большая” говорит не об абсолютном значении функции, а о характере его изменения в окрестности рассматриваемой точки. Никакое постоянное число, как бы велико оно ни было по абсолютному значению, не является бесконечно большим.

Примеры

1. Функция %%f(x) = 1/x%% — б.б. при %%x \to 0%%.
2. Функция %%f(x) = x%% — б.б. при %%x \to \infty%%.

Если выполнены условия определений $$ \begin{array}{l} \lim\limits_{x \to a}{f(x)} = +\infty, \\ \lim\limits_{x \to a}{f(x)} = -\infty, \end{array} $$

то говорят о положительной или отрицательной б.б. при %%a%% функции.

Пример

Функция %%1/{x^2}%% — положительная б.б. при %%x \to 0%%.

Связь между б.б. и б.м. функциями

Если %%f(x)%% — б.б. при %%x \to a%% функция, то %%1/f(x)%% — б.м.

при %%x \to a%%. Если %%\alpha(x)%% — б.м. при %%x \to a%% функция, отличная от нуля в некоторой проколотой окрестности точки %%a%%, то %%1/\alpha(x)%% — б.б. при %%x \to a%%.

Свойства бесконечно больших функций

Приведем несколько свойств б.б. функций. Эти свойства непосредственно следуют из определения б.б. функции и свойств функций, имеющих конечные пределы, а также из теоремы о связи между б.б. и б.м. функциями.

1. Произведение конечного числа б.б. функций при %%x \to a%% есть б.б. функция при %%x \to a%%. Действительно, если %%f_k(x), k = \overline{1, n}%% — б.б. функции при %%x \to a%%, то в некоторой проколотой окрестности точки %%a%% %%f_k(x) \ne 0%%, и по теореме о связи б.б. и б.м. функций %%1/f_k(x)%% — б.м. функция при %%x \to a%%. Получается %%\displaystyle\prod^{n}_{k = 1} 1/f_k(x)%% — б.м функция при %%x \to a%%, а %%\displaystyle\prod^{n}_{k = 1}f_k(x)%% — б.б. функция при %%x \to a%%.
2. Произведение б.б. функции при %%x \to a%% и функции, которая в некоторой проколотой окрестности точки %%a%% по абсолютному значению больше положительной постоянной, есть б.б. функция при %%x \to a%%. В частности, произведение б.б. функции при %%x \to a%% и функции, имеющей в точке %%a%% конечный ненулевой предел, будет б.б. функцией при %%x \to a%%.

Сумма ограниченной в некоторой проколотой окрестности точки %%a%% функции и б.б. функции при %%x \to a%% есть б.б. функция при %%x \to a%%.

Например, функции %%x - \sin x%% и %%x + \cos x%% — б.б. при %%x \to \infty%%.

3. Сумма двух б.б. функций при %%x \to a%% есть неопределенность. В зависимости от знака слагаемых характер изменения такой суммы может быть самым различным.

   Пример

   Пусть даны функции %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% — б.б. функции при %%x \to \infty%%. Тогда:

   • %%f(x) + g(x) = 3x%% — б.б. функция при %%x \to \infty%%;
   • %%f(x) + h(x) = 0%% — б.м. функция при %%x \to \infty%%;
   • %%h(x) + v(x) = \sin x%% не имет предела при %%x \to \infty%%.

Функция называется бесконечно малой при
или при
, если
или
.

Например: функция
бесконечно малая при
; функция
бесконечно малая при
.

Замечание 1. Никакую функцию без указания направления изменения аргумента бесконечно малой назвать нельзя. Так, функция
при
является бесконечно малой, а при
она уже не является бесконечно малой (
).

Замечание 2. Из определения предела функции в точке, для бесконечно малых функций выполняется неравенство
.Этим фактом мы в дальнейшем будем неоднократно пользоваться.

Установим некоторые важные свойства бесконечно малых функций.

Теорема (о связи функции, её предела и бесконечно малой): Если функция
может быть представлена в виде суммы постоянного числаА и бесконечно малой функции
при
, то число

Доказательство:

Из условия теоремы следует, что функция
.

Выразим отсюда
:
. Поскольку функция
бесконечно малая, для неё справедливо неравенство
, тогда для выражения (
) также выполняется неравенство

А это значит, что
.

Теорема (обратная): если
, то функция
может быть представлена в виде суммы числаА и бесконечно малой при
функции
, т.е.
.

Доказательство:

Так как
, то для
выполняется неравенство
(*) Рассмотрим функцию
как единую и неравенство (*) перепишем в виде

Из последнего неравенства следует, что величина (
) является бесконечно малой при
. Обозначим её
.

Откуда
. Теорема доказана.

Теорема 1 . Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Доказательство:

Проведём доказательство для двух слагаемых, так как для любого конечного числа слагаемых оно приводится аналогично.

Пусть
и
бесконечно малые при
функции и
– сумма этих функций. Докажем, что для
, существует такое
, что для всехх , удовлетворяющих неравенству
, выполняется неравенство
.

Так как функция
бесконечно малая функция,
, что для всех
выполняется неравенство
.

Так как функция
бесконечно малая функция,
, а следовательно существует такое, что для всех
выполняется неравенство
.

Возьмём равным меньшему из чисели, тогда в–окрестности точкиа будут выполняться неравенства
,
.

Составим модуль функции
и оценим его значение.

То есть
, тогда функция бесконечно малая, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции
при
на ограниченную функцию
есть бесконечно малая функция.

Доказательство:

Так как функция
ограниченная, то существует такое положительное число
, что для всехвыполняется неравенство
.

Так как функция
бесконечно малая при
, то существует такая–окрестность точки, что для всехих этой окрестности выполняется неравенство
.

Рассмотрим функцию
и оценим её модуль

Итак
, а тогда
– бесконечно малая.

Теорема доказана.

Теоремы о пределах.

Теорема 1. Предел алгебраической суммы конечного числа функций равен алгебраической сумме пределов этих функций

Доказательство:

Для доказательства достаточно рассмотреть две функции, это не нарушит общности рассуждений.

Пусть
,
.

По теореме о связи функции, её предела и бесконечно малой, функции
и
можно представить в виде
где
и
– бесконечно малые при
.

Найдём сумму функций
и

Величина
есть постоянная величина,
– величина бесконечно малая. Таким образом, функция
представлена в виде суммы постоянной величины и бесконечно малой функции.

Тогда число
является пределом функции
, т.е.

Теорема доказана.

Теорема 2 . Предел произведения конечного числа функций равен произведению пределов этих функций

Доказательство:

Не нарушая общности рассуждений, проведём доказательство для двух функций
и
.

Пусть , тогда
,

Найдём произведение функций
и

Величина
есть постоянная величина,бесконечно малая функция. Следовательно, число
является пределом функции
, то есть справедливо равенство

Следствие:
.

Теорема 3. Предел частного двух функций равен частному пределов этих функций, если предел знаменателя отличен от нуля

.

Доказательство: Пусть
,

Тогда
,
.

Найдём частное и проделаем над ним некоторые тождественные преобразования

Величина постоянная, дробь
бесконечно малая. Следовательно, функцияпредставлена в виде суммы постоянного числа и бесконечно малой функции.

Тогда
.

Замечание. Теоремы 1–3 доказаны для случая
. Однако, они могут быть применимы при
, поскольку доказательство теорем в этом случае проводится аналогично.

Например. Найти пределы:

Первый и второй замечательные пределы.

Функция не определена при
. Однако её значения в окрестности точки нуль существуют. Поэтому можно рассматривать предел этой функции при
. Этот предел носит названиепервого замечательного предела .

Он имеет вид:
.

Например . Найти пределы: 1.
. Обозначают
, если
, то
.
; 2.
. Преобразуем данное выражение так, чтобы предел свёлся к первому замечательному пределу.
; 3..

Рассмотрим переменную величину вида
, в которойпринимает значения натуральных чисел в порядке их возрастания. Дадимразличные значения: если

Давая следующие значения из множества
, нетрудно увидеть, что выражение
при
будет
. Более того, доказывается, что
имеет предел. Этот предел обозначается буквой:
.

Число иррациональное:
.

Теперь рассмотрим предел функции
при
. Этот предел называетсявторым замечательным пределом

Он имеет вид
.

Например.

а)
. Выражение
заменим произведениемодинаковых сомножителей
, применим теорему о пределе произведения и второй замечательный предел; б)
. Положим
, тогда
,
.

Второй замечательный предел используется взадаче о непрерывном начислении процентов

При начислении денежных доходов по вкладам часто пользуются формулой сложных процентов, которая имеет вид:

,

где - первоначальный вклад,

- ежегодный банковский процент,

- число начислений процентов в год,

- время, в годах.

Однако, в теоретических исследованиях при обосновании инвестиционных решений чаще пользуются формулой экспоненциального (показательного) закона роста

.

Формула показательного закона роста получена как результат применения второго замечательного предела к формуле сложных процентов

Непрерывность функций.

Рассмотрим функцию
определённую в некоторой точкеи некоторой окрестности точки. Пусть в указанной точке функция имеет значение
.

Определение 1. Функция
называется непрерывной в точке , если она определена в окрестности точки, включая саму точку и
.

Определение непрерывности можно сформулировать иначе.

Пусть функция
определена при некотором значении,
. Если аргументудать приращение
, то функция получит приращение

Пусть функция в точке непрерывна (по первому определению непрерывности функции в точке),

То есть, если функция непрерывна в точке , то бесконечно малому приращению аргумента
в этой точке соответствует бесконечно малое приращение функции.

Справедливо и обратное предложение: если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, то функция непрерывна.

Определение 2. Функция
называется непрерывной при
(в точке), если она определена в этой точке и некоторой её окрестности и если
.

Учитывая первое и второе определение непрерывности функции в точке можно получить следующее утверждение:

или
, но
, тогда
.

Следовательно, для того чтобы найти предел непрерывной функции при
достаточно в аналитическое выражение функции вместо аргументаподставить его значение.

Определение 3. Функция, непрерывная в каждой точке некоторой области называется непрерывной в этой области.

Например:

Пример 1. Доказать, что функция
непрерывна во всех точках области определения.

Воспользуемся вторым определением непрерывности функции в точке. Для этого возьмём любое значение аргумента и дадим ему приращение
. Найдём соответствующее приращение функции

Пример 2. Доказать, что функция
непрерывна во всех точкахиз
.

Дадим аргументу приращение
, тогда функция получит приращение

Найдём так как функция
, то есть ограничена.

Аналогично можно доказать, что все основные элементарные функции непрерывны во всех точках области их определения, то есть область определения элементарной функции совпадает с областью её непрерывности.

Определение 4. Если функция
непрерывна в каждой точке некоторого интервала
, то говорят, что функция непрерывна на этом интервале.